Flow of inference for Z-SINDy [1]. From the observed nonlinear dynamics we compute numerical derivatives and nonlinear library functions. Each set of library functions is associated with a free energy that determines the fit landscape.
The advent of big data about dynamical systems stimulated the development of data-driven modeling approaches aiming to extract concise system descriptions in form of nonlinear governing equations. While some applications are satisfied with with black-box neural network based models, for others it is increasingly important to identify equations that are human-interpretable and generalizable. Such algorithms aim to balance the quality of fit with the model parsimony, and thus their success generically depends on both the parameters of the dataset (length, sampling frequency, noise level) and the hyperparameters of the algorithm (resolution and sparsity).
In paper [1] below we cast system identification in Bayesian terms and analyze it with statistical mechanics tools to paint a detailed picture of the algorithmic failure as a phase transition.
[back to top]
Papers:
Statistical Mechanics of Dynamical System Identification, A. A. Klishin, J. Bakarji, J. Nathan Kutz, Krithika Manohar, arXiv:2403.01723, [pdf]
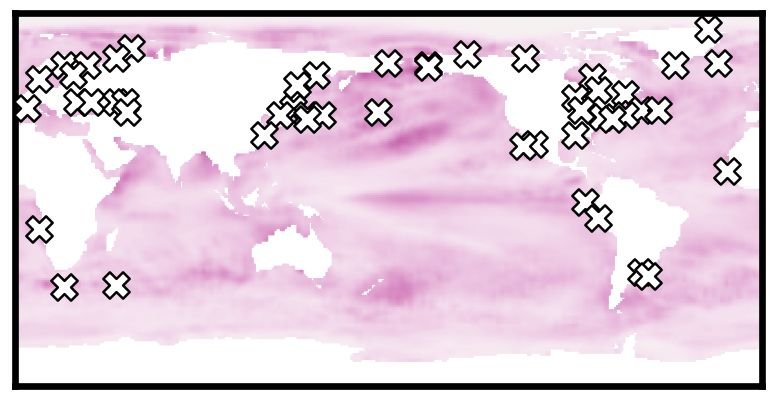
Data-driven sensors selected for the Sea Surface Temperature dataset (white markers) plotted over the temperature field reconstruction uncertainty [1].
When we observe complex, high-dimensional systems, we have to measure every single variable, but the resulting patterns don't have too much variation and are quite similar to each other. In technical terms, such signals are "sparse" and can be represented as a combination of just a few modes. The sparsity property is remarkable, because it allows reconstructing the whole system state from just a few local measurements. In statistics and signal processing this technique has been known under the name "compressed sensing", but if we have access to the training data of full system snapshots, we can use "sparse sensing" for even better reconstructions. Each local measurement is collected by a sensor, and choosing the sensor locations can make or break the state reconstruction. Previous approaches first chose sensors randomly, and then came up with clever greedy optimization techniques that identify the singular "best" configuration.
In paper [1] below, we look at the sensor placement problem through the lens of thermodynamics, compute the sensor interaction landscapes directly from the training data, and demonstrate state reconstructions for several empirical and synthetic datasets. In paper [2] below, we apply sensor placement methods to problems of digital twins of nuclear power plants.
[back to top]
Papers:
Data-Induced Interactions of Sparse Sensors, A. A. Klishin, J. Nathan Kutz, Krithika Manohar, arXiv:2307.11838, [pdf]
Leveraging Optimal Sparse Sensor Placement to Aggregate a Network of Digital Twins for Nuclear Subsystems, N. Karnik, C. Wang, P. K. Bhowmik, J. J. Cogliati, S. A. Balderrama Prieto, C. Xing, A. A. Klishin, R. Skifton, M. Moussaoui, C. P. Folsom, J. J. Palmer, P. Sabharwall, K. Manohar, M. G. Abdo, Energies, 17(13):3355 (2024), [pdf]
When presented with the network A, a human is likely to remember a shuffled version of it f(A). By emphasizing the within-module edges in network A*, we make the learned network f(A*) closer to the intended network A [1].
Across a variety of domains of human knowledge, from language to music to mathematics, the interconnected set of knowledge pieces is best represented as a complex network. However, once we attempt to communicate our knowledge to others, we are faced with a limited communication channel. Often the best we can do is to transmit a one-dimensional sequence of signals so that the recipient decodes the message from correlations in this sequence. Such decoding is subject to noise and mental errors such as random shuffling, which nevertheless can be characterized statistically. The varied ways of communicating networks that account for quirks of human brain form the interdisciplinary field of graph learning.
In paper [1] below, we show that intentionally misrepresenting the networks by emphasizing some connections over others can rectify the shuffling effect somewhat, which opens opportunities to design educational materials. In paper [2], we propose a theory for graph learning with random walks of finite length that leads to incomplete exploration and distorted structure. In paper [3], we extend the graph learning theory to account for the mental errors characteristic of humans. In paper [4], we consider how humans learn multiple hierarchical levels of networks.
[back to top]
Papers:
Optimizing the Human Learnability of Abstract Network Representations, W. Qian, C. W. Lynn, A. A. Klishin, J. Stiso, N. H. Christianson, D. S. Bassett, Proceedings of the National Academy of Sciences, 119.35 (2022): e2121338119, arXiv:2111.12236, [pdf], [pdf SM]
Exposure theory for learning complex networks with random walks, A. A. Klishin and D. S. Bassett, Journal of Complex Networks, 10.5 (2022): cnac029, arXiv:2202.11262, [pdf]
Learning Dynamic Graphs, Too Slow, A. A. Klishin, N. H. Christianson, C. S. Q. Siew, D. S. Bassett, arXiv:2207.02177
Human Learning of Hierarchical Graphs, X. Xia, A. A. Klishin, J. Stiso, C. W. Lynn, A. E. Kahn, L. Caciagli, D. S. Bassett, Phys. Rev. E, 109, 044305, arXiv:2309.02665, [pdf]
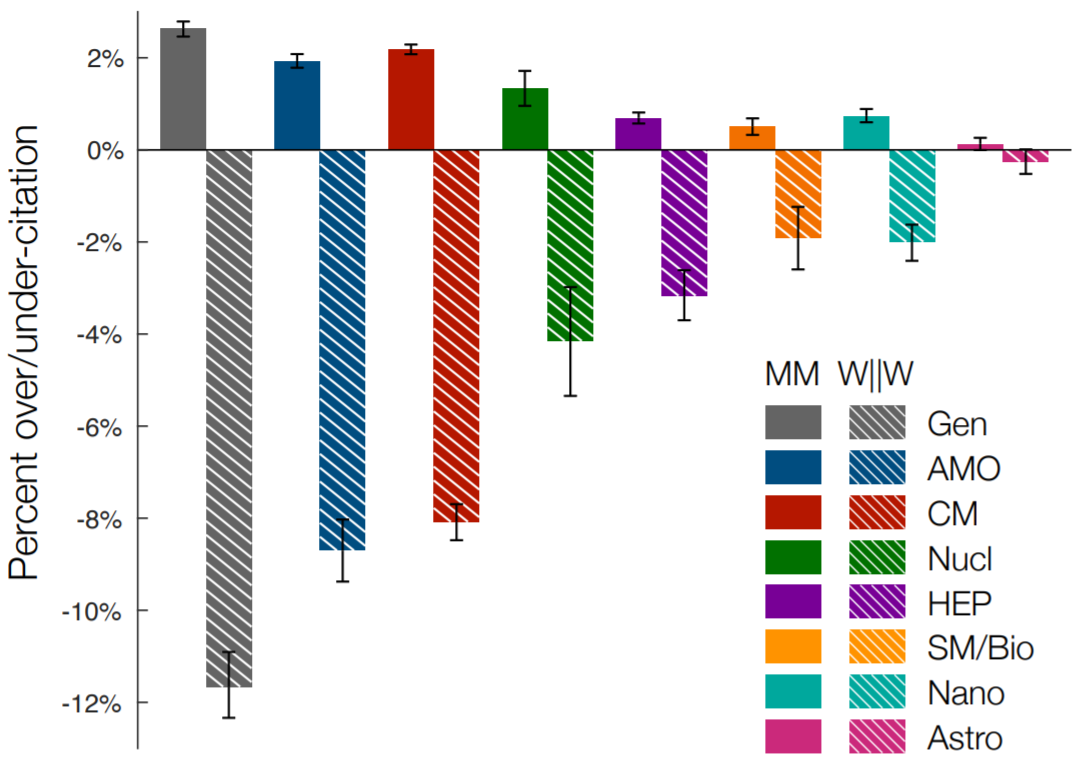
Across a range of physics subfields, articles where both first and last author are men (MM) are consistently overcited with respect to expected citation rate, while articles with at least the first or last woman author (W||W) are consistently undercited. The inequity varies by the specific subfield, being the most dire in general physics, and comparatively smaller in astronomy [1].
The historical and contemporary under-attribution of women’s contributions to scientific scholarship is well-known and well-studied, with effects that are felt today in myriad ways by women scientists. One measure of this under-attribution is the so-called citation gap between men and women: the under-citation of papers authored by women relative to expected rates coupled with a corresponding over-citation of papers authored by men relative to expected rates. We explore the citation gap in contemporary physics, analyzing over one million articles published over the last 25 years in 35 physics journals that span a wide range of subfields. Using a model that predicts papers’ expected citation rates according to a set of characteristics separate from author gender, we find a global bias wherein papers authored by women are significantly under-cited, and papers authored by men are significantly over-cited. Moreover, we find that citation behavior varies along several dimensions, such that imbalances differ according to who is citing, where they are citing, and how they are citing. Specifically, citation imbalance in favor of man-authored papers is highest for papers authored by men, papers published in general physics journals, and papers likely to be less familiar to citing authors. Our results suggest that, although deciding which papers to cite is an individual choice, the cumulative effects of these choices needlessly harm a subset of scholars. We discuss several strategies for the mitigation of these effects, including conscious behavioral changes at the individual, journal, and community levels.
[back to top]
Papers:
Citation inequity and gendered citation practices in contemporary physics, E. G. Teich, J. Z. Kim, C. W. Lynn, S. C. Simon, A. A. Klishin, K. P. Szymula, P. Srivastava, L. C. Bassett, P. Zurn, J. D. Dworkin, D. S. Bassett, Nature Physics, 18.10 (2022): 1161-1170, arXiv:2112.09047, [pdf], [pdf SM]
Complex systems design raises questions about the paterns of arrangement across the whole ensemble of possible design solutions. Systems Physics allows, among other things, mapping out these patterns, such as avoidance, adjacency, and association [3].
The main arc of my Ph.D. work has been development of Systems Physics, a framework to study design problems of distributed systems alternative to, and broader than, optimization [4]. Design problems are inherently wicked problems: that is, the design objectives are themselves ill-defined, and cannot be understood without already having the solutions. Systems Physics takes the perspective of statistical mechanics and naturally accounts for combinatorially large solution spaces and shifting design pressures. I mainly applied this perspective to ship design problems from Naval Engineering. Systems Physics has allowed us to uncover phase transitions between wide classes of solutions [1], evaluate robustness of viable architecture classes [2], describe emergent patterns in the ensembles of system arrangements early in the design process [3], and establish a “no free lunch” result for clustering in distributed systems [5].
[back to top]
Papers:
Statistical Physics of Design, A. A. Klishin, C. P. F. Shields, D. J. Singer, and G. van Anders, New J. Phys., 20.10 (2018): 103038, arXiv:1709.03388, [pdf], [pdf SM]
Robust Design from Systems Physics, A. A. Klishin, A. Kirkley, D. J. Singer, and G. van Anders, Scientific Reports, 10, 14334 (2020), arXiv:1805.02691, [pdf]
Avoidance, Adjacency, and Association in Distributed Systems Design, A. A. Klishin, D. J. Singer, and G. van Anders, Journal of Physics: Complexity, 2, 025015 (2021), arXiv:2010.00141, [pdf]
Statistical Physics of Design, A. A. Klishin, Ph.D. Thesis, University of Michigan (2020), [pdf]
No Free Lunch for Avoiding Clustering Vulnerabilities in Distributed Systems, P. Chitnelawong, A. A. Klishin, N. MacKay, D. J. Singer, G. van Anders, arXiv:2308.05196, [pdf]
(a) Self-assembly can produce structures of varying sequence, length, and topology. (b) The self-assembly design space is spanned by the binding energy, chemical potential, and bond rigidity. (c) All structures can be enumerated with techniques based on transfer matrices.
The dawn of 21st century showed a new way of creating materials and structures at nano- and micro-scale, via self-assembly. When making stuff out of atoms and molecules, one is beholden to quantum mechanics: there is no continuous transformation from nitrogen to oxygen atoms. Larger particles, however, have almost continuous degrees of freedom of shape, patchiness, and specific binding, thus opening a much wider design space than the discrete confines of the periodic table of elements. By designing specific particles, or sets of particles, we can "program" the matter to self-assemble into structures of our wishes.
My humble contribution to this topic is a study connecting the patterns of binding energies to the topology of formed structures, such as open chains or closed loops. Within the space of one-dimensional structures, I can able to enumerate all possible structures. This enumeration generically diverges - a fact only obvious to select seasoned field theorists. In the paper we show that treating chemical potential as an implicit parameter mitigates the divergence. This mitigation produces qualitative and quantitative design rules for what to put into the energy matrices, and what sizes of structures can be designed and assembled with a given specific binding platform.
[back to top]
Papers:
Topological Design of Heterogeneous Self-Assembly, A. A. Klishin and M. P. Brenner, submitted, arXiv:2103.02010
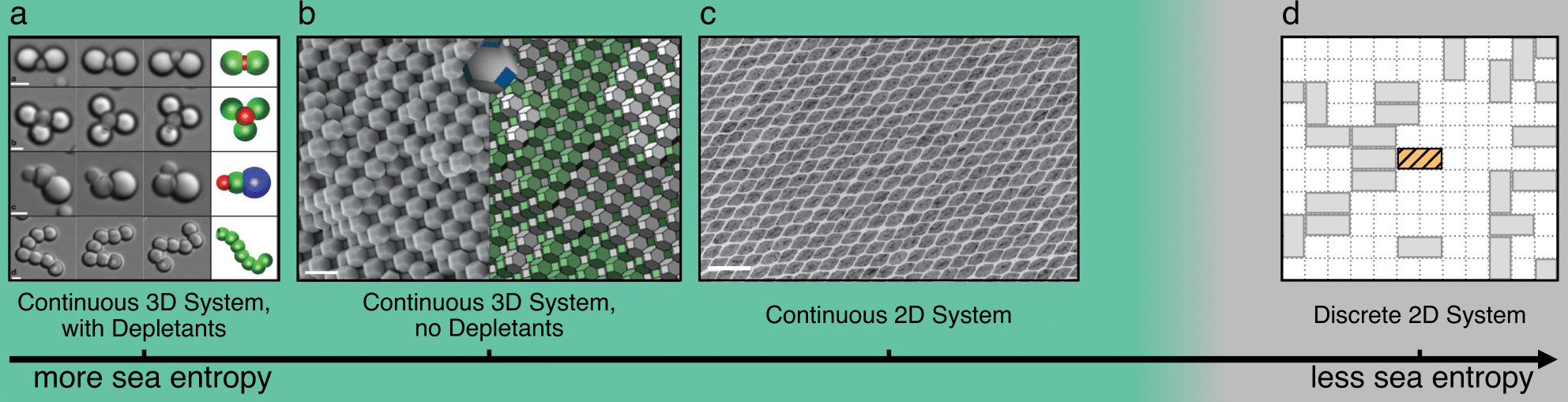
The word "entropy" was invented by Clausius to mean, in a special technical sense, the amount of disorder. In many systems, entropic randomization competes with energetic alignment resulting in a wide range of states of matter, from disordered gas to a perfect crystal. In some systems, however, entropy can be isolated and purified to become the sole causal mechanism. Since Onsager's liquid crystal models of the 1940s, and hard sphere crystallization simulations of the 1950s, numerous studies showed entropy alone leading to a robust ordering of matter. Surveying the diverse zoo of entropically ordered systems, we pondered: when does entropy promote local organization? What are the minimal conditions for that to happen?
All entropically ordering systems can be arranged on the axis of “sea entropy“, or the number of states that system can take if two particle positions are fixed. Sea entropy decreases from 3D particles with depletants (a), to 3D particles without depletants (b), to 2D particles in continuous space (c), to, finally, 2D particles on a lattice (d). Measuring entropic ordering in (d) thus provides a lowest bound and sufficient condition for the whole axis.
We address this question by taking an entropic system and stripping it from most of its entropy: confined to a plane, with no continuous rotations or translations. The resulting lattice dimer system is one of the oldest statistical mechanics models. While the "dawn of computational physics" is an ill-defined reference to a historical period, at one of those dawns in the 1930s the recurrence relations for the lattice dimer counting problem were studied on the Mallock machine, an early analog computer. The model was "solved" simultaneously in several tour de force papers in 1961 (in the 1960s sense of the word "solved"). In our paper we study the last dark corner of this model: local motifs at finite dimer density. We show that entropic ordering persists even in this most restricted system, and formulate a set of sufficient conditions for entropy to promote local organization.
[back to top]
Papers:
When Does Entropy Promote Local Organization?, A. A. Klishin and G. van Anders, Soft Matter, (2020), 16, 6523-6531,
[pdf], [pdf ESI]
Tensor networks form an information structure about the design space. While the initial topology (a) computes the partition function Z, we can add various modifications (bcd), and recombine them into specific queries (efg) yielding knowledge about the design space.
Apart from answering interesting scientific questions, I develop new statistical mechanics methods that allow posing these questions in new and insightful forms. A statmech ensemble can be cast as an information structure, or an algebraic object from which we can extract knowledge with computable queries. A particular information structure that I adapted for my work is a tensor network, where the nodes are tensors and the edges are the pattern of their contractions.
In the paper [1] below, I needed to compute the properties of a system with both a nontrivial spatial structure and a complex, but fixed topology. I introduced tensor networks as a comprehensive graphical language for conditioning and marginalizing variables and modifying couplings between them. The resulting diagrammatic expressions are more compact and interpretable than corresponding algebraic formulas. This helps interpreting calculations, much like Feynman diagrams surpassed bulky integral expressions and became part of the standard language of field theory.
In the paper [2] below, I needed to evaluate the subtle Directional Entropic Forces in a lattice dimer model. Computing the entropy required enumerating an astronomical number of combinations of states (up to 10^167 in the paper) and counting the ones that satisfy a set of local constraints. I introduced a tensor network formulation that performs this counting and extracts many one-point functions simultaneously with a technique called multi-marginalizing.
I show that tensor networks are a convenient language for discussing the interplay of local couplings, interaction topology, and global properties in a large range of systems. I am sure that numerical methods for tensor network manipulations and computations will steadily improve in the coming years as they have for quantum lattice-based systems, the most popular tensor network application area.
[back to top]
Papers:
Avoidance, Adjacency, and Association in Distributed Systems Design, A. A. Klishin, D. J. Singer, and G. van Anders, Journal of Physics: Complexity, 2, 025015 (2021), arXiv:2010.00141, [pdf]
When Does Entropy Promote Local Organization?, A. A. Klishin and G. van Anders, Soft Matter, (2020), 16, 6523-6531,
[pdf], [pdf ESI]
Software:
Lachesis, P. Chitnelawong, A. A. Klishin, N. MacKay, G. van Anders, Zenodo.8088164 (2023)
Accretion of new parcels of mass (square) to existing dense cores (circles) is driven by both the distance between them and their mass, akin to preferential attachment in network models. This interplay, combined with the fractal distribution in space, yields the power-law distribution of star masses.
One of the central problems in the study of star formation is the Initial Mass Function (IMF), or distribution of stars in a cluster by mass. Observations and numerical simulations suggest that the distribution has a power law shape over several decades in mass, but it is unclear what causes that characteristic shape and how to explain the universality of the power law exponent across clusters. In the paper below we directly model the Dense Cose Mass Function (CDMF, a precursor to IMF) by treating the competitive accretion of mass onto dense cores analogously to preferential attachment models in network theory. We connect the spatial distribution of stars and accreting mass to the fractal statistics of turbulent interstellar medium. This theory predicts the universal power law exponent and matches the observations over three decades in mass.
[back to top]
Papers:
Explaining the stellar initial mass function with the theory of spatial networks, A. A. Klishin and I. Chilingarian, The Astrophysical Journal, 824, 1 (2016), arXiv:1511.05200, [pdf]